Early Stages of Mineral Formation in Water: From Ion Pairs to Crystals

1811 5209/25/0021 0018$2.50 DOI: 10.2138/gselements.21.1.18

Keywords: mineral formation; ion pairs; charged triple-ion clusters; pre-nucleation clusters; nucleation; amorphous precursors

INTRODUCTION

Mineral precipitation from aqueous solutions occurs in a wide variety of geological, biological, and industrial systems, and plays important roles in several cross-disciplinary fields (see the first chapter of this issue). It can occur when the solution is supersaturated with respect to a specific mineral, i.e., the solution contains more than the allowed maximum amount of dissolved ions, according to their solubility constants at a given temperature and pressure.

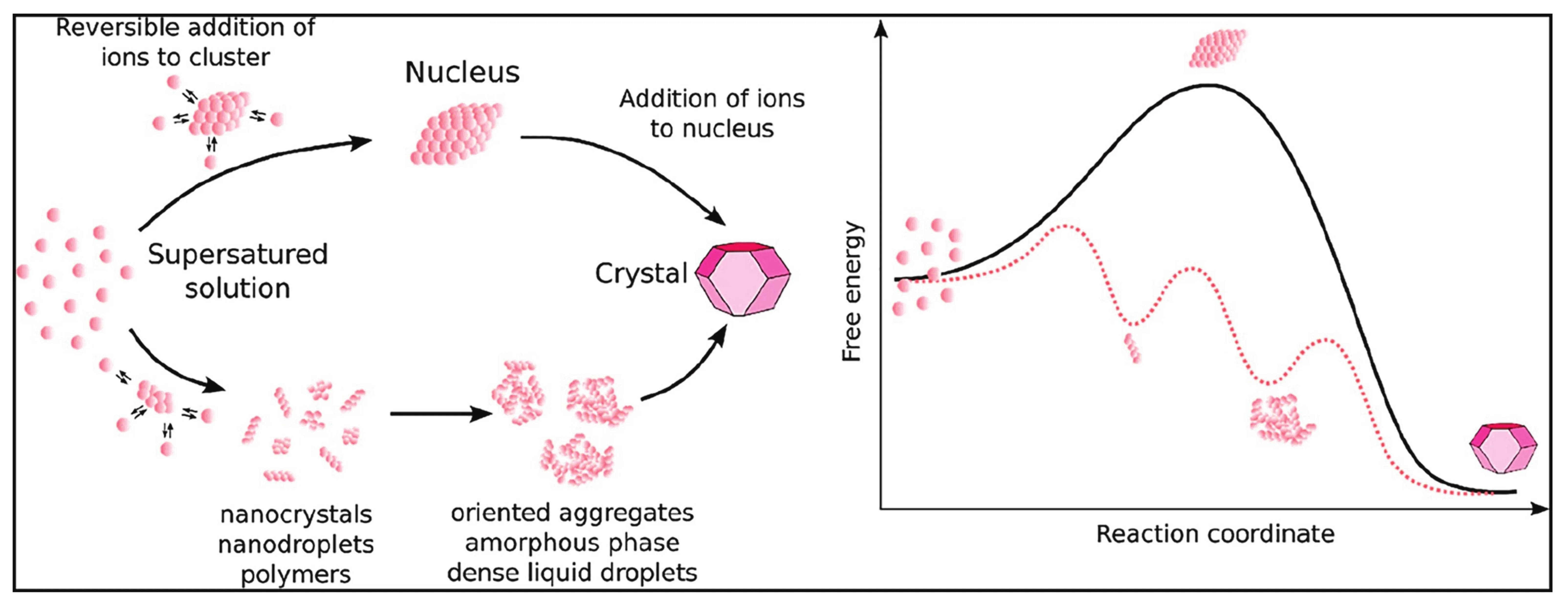
The thermodynamic driving force for mineral nucleation and growth is the difference in the chemical potential between the dissolved single ions and the final stable solid state. This can be envisaged as an overall downslope route through a mountainous free energy landscape. The “free” dissolved ions are in one of the valleys, and they can hike up or downslope along different routes, encountering other valleys before reaching the mountain base. The valleys along the way represent energy minima for different intermediate species, dissolved or solid, and the lowest base represents the final stable mineral crystal. Free energy profiles (e.g., Fig. 1) are like the mountain profile the ions hiked from the dissolved state via intermediate species to the final crystal. On the contrary, in an undersaturated solution, the valley for the dissolved ions would lie lower than that for the crystals, which would dissolve. Thus, depending on the level of supersaturation, different pathways are thermodynamically possible (i.e., going from high to low elevation), which may or may not include intermediate valleys. Indeed, the understanding of this free energy landscape can be hampered by the lack of knowledge of intermediate species, which are formally neglected when calculating the degree of supersaturation (Gebauer et al. 2018). The latter is based solely on the ratio between the ion activity product (IAP), which is the product of the activities (or “effective concentrations” measured as deviation from the chosen standard state) of the freely dissolved ions involved and the solubility of the final solid. Higher IAP values are associated with higher degrees of supersaturation. The elevation of a given valley contains no information on interjacent valleys. Additionally, mineral precipitation depends on kinetics, that is, mountains in between valleys, which reflects the lifetimes and formation rates of all clusters, initially precipitated solids and nanoparticles (precursors and intermediates), and the final solid. The formation mechanism of clusters and precursors, and the effect of additives and physicochemical factors on their formation, are currently not fully captured by any comprehensive theory.

Decades of study in this area have revealed numerous possible nucleation mechanisms (De Yoreo et al. 2015), involving clusters, and precursor phases that can lead to one or a range of mineral phases (not necessarily the thermodynamically stable one), depending on the physicochemical conditions and the presence of additives (Gower 2008; Meldrum and Cölfen 2008). Major advances have been achieved in defining the role of aqueous aggregates of minerals, the formation mechanisms of different crystalline phases sharing the same formula unit (polymorphs), of distinct amorphous forms, hydrated crystalline phases, and of complex hierarchical structures such as mesocrystals (Jehannin et al. 2019). This is thanks to the rapid development of experimental techniques that are able to probe nucleation steps (e.g., Van Driessche et al. 2019; Gebauer et al. 2022) and, simultaneously, the fast evolution and broad availability of cutting-edge computing infrastructures in conjunction with major advances in the methods that allow accurate modeling of minerals and mineral–fluid interfaces at the atomic and electronic scale (Byrne et al. 2017; Schuitemaker et al. 2024).

While a general, comprehensive theory that covers all aspects of mineral nucleation is not available, over the last decade, the idea that mineral nucleation can occur via mechanisms that are alternative to those envisaged by the classical nucleation theory has become well established, to a point that we can confidently refer to a non-classical nucleation theory. The fundamental difference between classical and non-classical nucleation theory lays in the free energy profile associated with the process. Figure 1 shows that classical nucleation theory predicts a single nucleation step with an activation barrier that can be overcome when the radius of the mineral nucleus reaches a critical size. Non-classical nucleation occurs in multiple steps involving (meta-)stable clusters and precursors that inhabit local free energy minima, separated by multiple activation barriers that do not necessarily depend on supersaturation, and/ or may easily be overcome at ambient thermal energies (Gebauer et al. 2022).

In this article, we focus on advances over the last two decades on the early stages of mineral nucleation in water. Part of our discussion focuses on calcium-carbonate, as it is the most abundant and most often studied (bio)mineral, important in various geochemical and industrial contexts. Some other mineral systems are discussed as alternative examples. We start with an overview of the earliest and most elementary process—the formation of an ion pair— and proceed via larger-size prenucleation clusters to the formation of (amorphous or crystalline) solids. We point the readers to the remainder of this special issue for more advanced stages of nucleation and crystal growth.

ION PAIRS

The very first step in mineral/crystal nucleation in an aqueous medium is the association of dissolved ions into ion pairs. Even this elementary event is more complex than might be expected. Using computational techniques as “theoretical microscopes” to look at this process with an atomic-size lens has helped reveal the association mechanisms in detail.

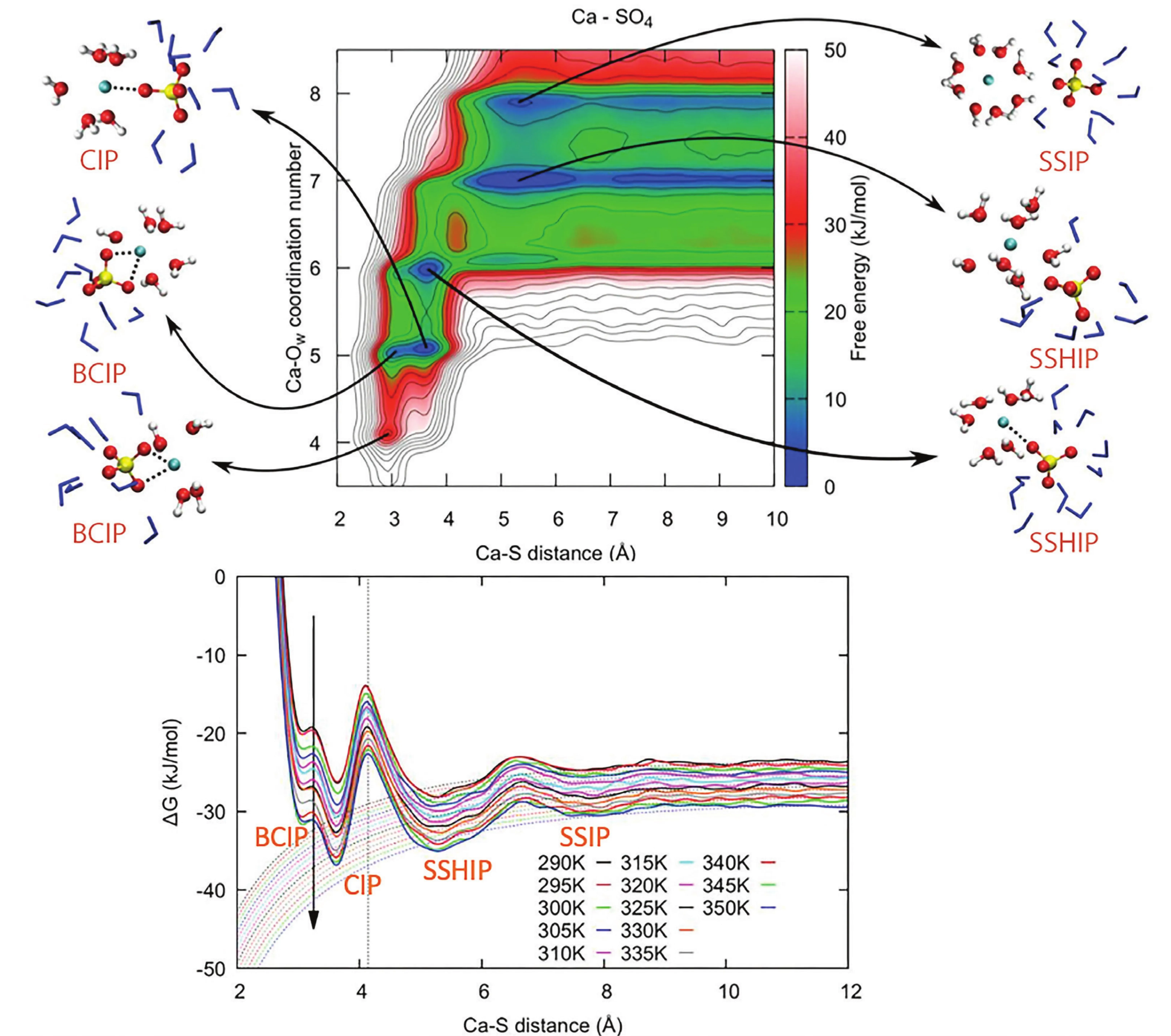
Freely dissolved ions have a shell of coordinated water molecules around them, the solvation shell. Typically, an ion pairing event occurs through different steps with progressively less water molecules between the ions (Byrne et al. 2017). Each of these steps is associated to a free energy minimum, a valley on the above mentioned downhill slope, leading to a free energy profile characterized by the following energy minima (Fig. 2):

1. solvent-separated ion pair (SSIP), where the two ions interact via both of their solvation shells;
2. solvent-shared ion pair (SSHIP), where the two ions share part of their solvation shell;
3. contact ion pair (CIP), with at least one direct interaction between the two ions.
Depending on the nature of the ion pair, there could be additional minima related to mono- and poly-dentate binding with larger oxyanions (e.g., CO3 2−, SO4 2−, HPO4 2−), where more than one bond can be formed. Figure 2 shows the example of a calcium sulfate ion pair, with an additional bidentate contact ion pair (BCIP). An even more complex case of ion pairing is discussed in Schuitemaker et al. (2024) for calcium aspartate, with multiple binding sites and flexibility of the aspartate molecule.

CHARGED TRIPLE ION CLUSTERS

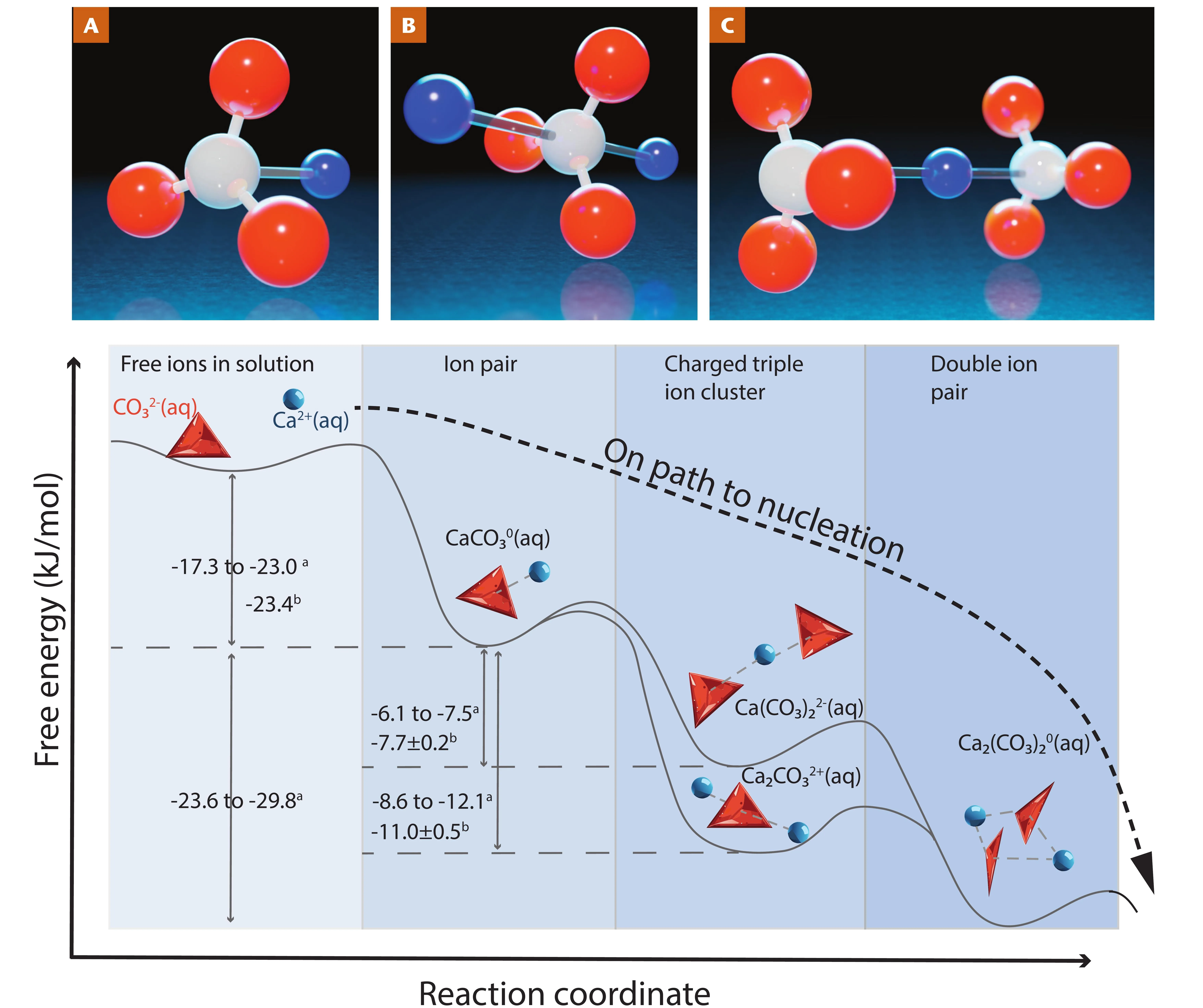
The next step after ion pair formation is the growth of these pairs. This can occur via addition of single ions or chargeneutral ion pairs. When a third ion binds to an ion pair (Fig. 3A), a triple ion cluster (TIC) is formed. Often, they are charged (CTIC). For calcium carbonate, they are either positively charged (i.e., [Ca2CO3]2+, Fig. 3B) or negatively charged (i.e., [Ca(CO3)2]2−, Fig. 3C).
CTIC species are common in aqueous solutions of metal cations (cf. thermodynamic databases such as for PHREEQC; Parkhurst and Appelo 2013). CTICs have been detected using mass spectrometry (nickel sulfates, Schröder et al. 2011) and Raman spectroscopy (magnesium sulfate, Rudolph et al. 2003), inferred from titrations and solubility measurements (iron sulfides, Rickard and Luther 2007), and investigated computationally (metal carbonates and sulfates, Raiteri et al. 2020; Koskamp et al. 2024).

Commonly, when (semi )ionic minerals form in aqueous environments, they do so from solutions that are nonstoichiometric. In other words, the concentration ratio

of the crystal-building ions is not the ideal (stoichiometric) ratio of the mineral. For example, in CaCO3, the Ca:CO3 ratio in the solid is 1:1, while it can vary more than five orders of magnitude in natural and engineered solutions (Seepma et al. 2021). In such conditions, the route for ion-pair growth is much more probable via addition of the excess ion than via ion pair addition.

Raiteri et al. (2020) and Koskamp et al. (2024) confirmed computationally and experimentally for the CaCO3 system that growth of the ion pair via calcium ion addition was thermodynamically more favorable than via carbonate ion addition (Fig. 3). Contrastingly, they showed for BaSO4 and other carbonates and sulfates that ion pair growth via anion addition was thermodynamically more favorable, in agreement with experimental observations (Seepma et al. 2023). These results strongly suggest that, depending on the solution composition, ion pairs and CTICs represent the smallest prenucleation clusters.

LARGER-SIZE PRENUCLEATION CLUSTERS

Over the past 20 years, nucleation mechanisms that differ from that predicted by classical nucleation theory (CNT) have been introduced. In 2008, Gebauer et al. demonstrated that stable associated states of ions beyond ion-pairing occur prior to nucleation of calcium carbonate, the so called pre-nucleation clusters (PNCs); for the original work and a detailed definition of PNCs, see Gebauer et al. (2014)
The occurrence of PNCs has been confirmed for various systems, including calcium phosphates (Dey et al. 2010), calcium sulfates (Van Driessche et al. 2019), iron and aluminium (oxyhydr)oxides, calcium silicate hydrates, proteins, and small organic molecules (Gebauer et al. 2014). Although part of the scientific community is still debating the occurrence and significance of PNCs (Smeets et al. 2017; Gebauer et al. 2018), it has become evident that the solvent—water—plays a key role in the PNC formation mechanism (Gebauer et al. 2022). The release of water molecules from solvation shells upon PNC formation

thermodynamically drives this process, due to a considerable entropic gain. The occurrence of PNCs may thus be more prevalent in aqueous systems than previously thought (Gebauer et al. 2022). PNCs are significantly more abundant than classical precritical nuclei, as their formation is associated with a negative free energy change (going downhill, Fig. 1), rather than positive as for (pre )critical nuclei (going uphill first, Fig. 1).

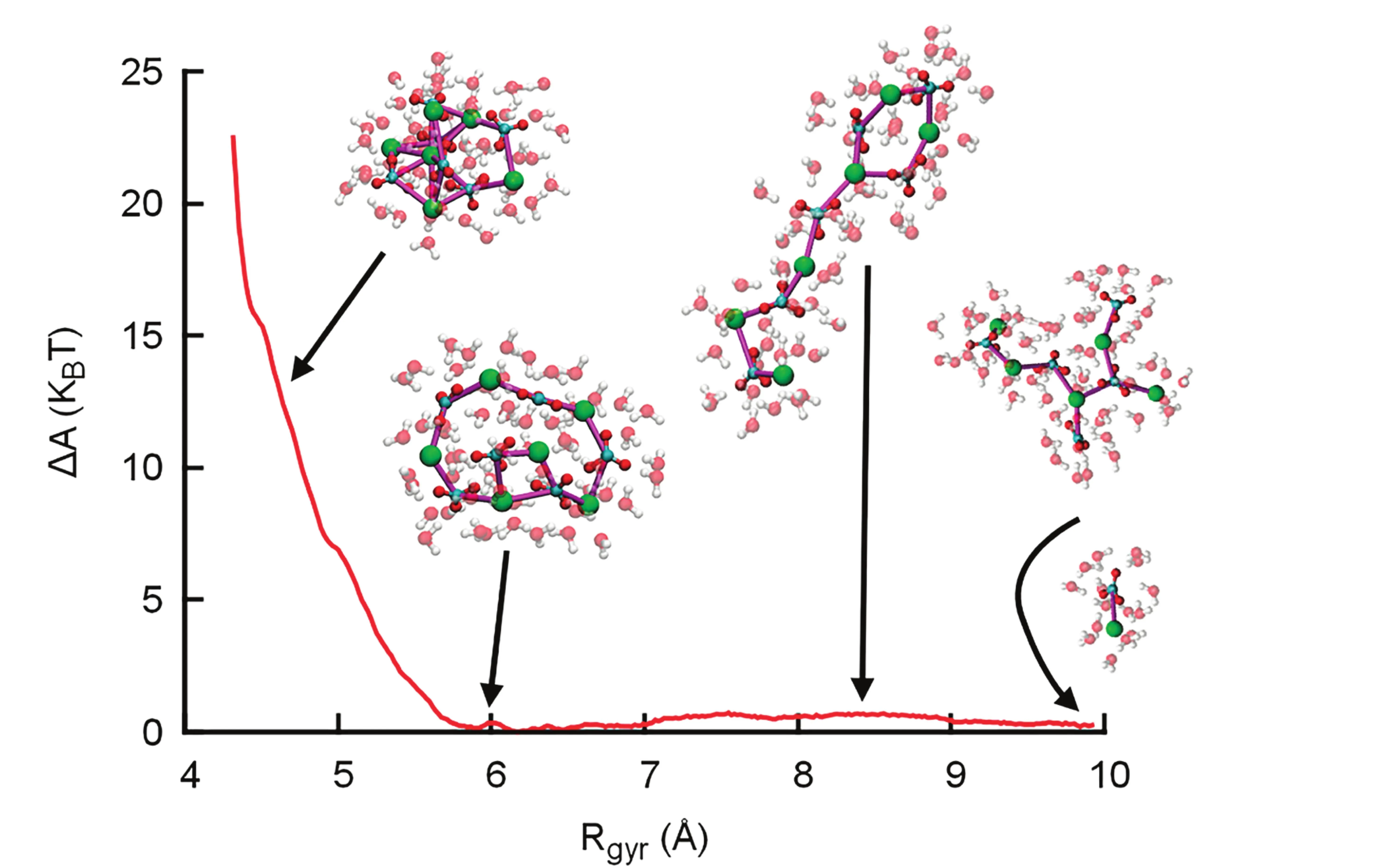
For calcium carbonate, atomistic insight into the structure and (thermo )dynamics of PNCs was obtained using computer simulations. Here, ion pair chains were observed and named DOLLOPs (dynamically ordered liquid like oxyanion polymers), due to their rapid evolution between linear, branched, and ring arrangements and their ability to rapidly change size and exchange ions with the solution (Demichelis et al. 2011). Contrastingly, more defined and less dynamic, highly anisotropic nanoclusters may occur (e.g., De Yoreo et al. 2015; Van Driessche et al. 2019). Formally, there is no solid–liquid interface between a chain-like cluster and a solution; additionally, the simulations suggest that ion exchange dynamics between PNCs and the solution are similar to solution dynamics, i.e. DOLLOPS are dissolved PNCs.

The results by Demichelis et al. (2011) suggest that a significant barrier for nucleation of bulk-like nanoparticles arises from the energetic costs of dehydrating DOLLOPs further (Fig. 4, left). This shows that PNCs cannot spontaneously transform into compact clusters—so how can PNCs mechanistically participate in phase separation? A possible answer was provided by Wallace et al. (2013), who suggested that higher coordination numbers in larger PNCs slow down the dynamics and thereby turn PNCs into nanodroplets. This event corresponds to liquid–liquid phase separation (LLPS): dense liquid droplet formation in a solvent (water), similar to the formation of an emulsion. Avaro et al. (2020) demonstrated that the PNC theory can explain and predict LLPS in the aqueous calcium carbonate system. The model captures the phenomenon of experimentally observed amorphous polymorphism (Cartwright et al. 2012), and quantitatively predicts the commonly accepted literature value for the solubility of amorphous calcium carbonate

(ACC) (Brečević and Nielsen 1989) based on the PNC theory, resolving previous debates (Gebauer et al. 2018). The model is general and can be tested and adapted for various systems in which PNCs occur (see above). However, the general explanatory and predictive power remains to be tested in the future—as is the case for CNT.

NUCLEATION OF SOLID MINERALS

Drawing a comprehensive picture of how minerals nucleate is non trivial due to the variety of conditions, chemicals, and intermediates involved, and to the complexity of the reaction environment and the mechanisms. Broadly speaking, this process can occur heterogeneously (i.e., on an existing surface) or homogeneously (i.e., in solution), and it cannot be excluded that “classical” mechanisms are at play under certain conditions, especially in heterogeneous scenarios. In essence, any process that is imaginable and physically possible can occur.

Such a complex scenario can be illustrated by remembering our mountain landscape, now expanded with countless valleys, representing different phases, and hills and mountains between them, where myriads of pathways exist. The route with the lowest elevation between two valleys would be the one that a reaction would most likely follow, similar to an efficient route for a hiker. From the perspective of nucleation and growth, the pathway with the lowest overall barrier is the active one.

However, the theoretical free energy landscape of nucleation and growth is more complicated than actual landscapes. Just like the occurrence of possible pathways (from high to low elevation) is governed by supersaturation as described above, the heights of free energy barriers depend on numerous parameters. These range from the chemical environment (additives, solution stoichiometry, ionic strength) to temperature, pressure, and the presence of interfaces. The technical term for this is “kinetic control”—how long does it take to go uphill and down to the next valley? Are there other hills that are easier to hike? Would they lead to a different valley, and how much lower is this valley compared to the others? The detailed elucidation of free energy landscapes, i.e., the kinetic control of nucleation and growth, is a formidable task. Computer simulations can help to address this dilemma through capturing atomic scale details of the first steps of the nucleation process, as described above. However, the full time and length scale of nucleation (miliseconds to hours and micro to millimeters) is beyond what is achievable with state-of-the art computing resources (nano to microseconds). As such, we resort here to briefly discussing selected experimental examples of nucleation pathways.

For a range of minerals, including calcium phosphates (Dey et al. 2010), carbonates (Brečević and Nielsen 1989), various metal oxides, and silica (as reviewed by Navrotsky 2004), amorphous precursor phases are frequently the first solid to form. In the case of calcium carbonate, ACC is a disordered, hydrated phase, with a water content between 0.5 to 1.5 H2O molecules per CaCO3 (Cartwright et al. 2012). In addition to the varying water content, distinct shortrange structures can be found relating to the different anhydrous crystalline polymorphs, which are thermodynamically controlled by pH and temperature (Cartwright et al. 2012; Avaro et al. 2020). While calcite is ultimately the most stable form of calcium carbonate at ambient temperature and pressure, Raiteri and Gale (2010) showed that ACC nanoparticles are more stable than calcite when the size of the particle is below ~4 nm. This is in line with what is observed for other minerals that exhibit phase stability changes at the nanoscale due to interfacial effects with solvent interactions becoming important (Navrotsky 2004). Because they may become thermodynamically stable below a certain size, amorphous solids could occur more generally, that is, beyond kinetic controls. Certainly, the transformation of amorphous forms, and later, the formation

of larger crystals, are under kinetic control though. For calcium carbonate, evidence suggests that transformation of ACC into crystals can involve dissolution/reprecipitation, which can be coupled at interfaces (Ruiz-Agudo et al. 2014), but also solid state transformation like mechanisms (Ihli et al. 2014). Nucleation barriers can be further influenced by the solution stoichiometry (Seepma et al. 2021) while interfacial charges of the forming nanoparticles are also affected (Seepma et al. 2023). Additionally, on the pathway to stable calcium carbonate crystals, a number of metastable, hydrated and anhydrous, crystalline phases may form, depending on the chemical environment and physical conditions, that would eventually transform into the stable structure. Another example of high pathway complexity is calcium sulfate (Van Driessche et al. 2019; see Fig. 5). Here, the process begins with the formation of highly anisotropic sub-3 nm primary species that subsequently assemble into loose domains, then densify, and later grow, coalesce, and order within the aggregates, finally transforming into crystalline gypsum (Stawski et al. 2019; Van Driessche et al. 2019). Similar stacking of sub-3 nm particles has also been inferred in the formation of iron monosulfides (Wolthers et al. 2003), and observed in other mineral systems (De Yoreo et al. 2015).

SUMMARY AND CONCLUSIONS

Mineral nucleation is an enigmatic process that can occur via a rich variety of dissolved and solid intermediate species/phases that have until recently been overlooked. Before the first solids precipitate, the crystal building ions can pair up, forming clusters of three or more ions. These are prenucleation clusters and they all inhabit their own gentle valley on the downward slope to solid formation. At sufficiently high ion concentrations, dense liquid mineral droplets in water may form, and further downslope, solids. These solids can be amorphous phases with distinct, disordered structures, assembling nanocrystals, metastable or stable nanocrystals that again inhabit their own valleys just above the deepest valley of the final large stable crystal. Depending on the conditions, its formation can therefore occur via one or more of these solid precursor phases, with dissolution/reprecipitation or recrystallisation processes helping the downhill transformation process along. Differences in physicochemical conditions, confinement, interfaces and additive concentrations impact the downhill route taken, and may lead to kinetic stabilization of intermediates occurring along the pathway. An overview of this impact is provided in the next chapters.

ACKNOWLEDGMENTS

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. [819588]) to MW. RD thanks the Australian Research Council for support though a Discovery Project (DP160100677) and a Future Fellowships (FT180100385), the Pawsey Supercomputing Centre, and the Australian National Computational Infrastructure for provision of computing time through the NCMAS and Pawsey Partners merit allocation schemes. Ton Markus is acknowledged for designing Figures 3A–3C and the banner figure.

REFERENCES

Avaro JT, Wolf SLP, Hauser K, Gebauer D (2020) Stable prenucleation calcium carbonate clusters define liquid–liquid phase separation. Angewandte Chemie International Edition 59: 6155-6159, doi: 10.1002/anie.201915350

Brečević L, Nielsen AE (1989) Solubility of amorphous calcium carbonate. Journal of Crystal Growth 98: 504-510, doi: 10.1016/0022-0248(89)90168-1

Byrne EH, Raiteri P, Gale JD (2017) Computational insight into calcium– sulfate ion pair formation. Journal of Physical Chemistry C 121: 25956-25966, doi: 10.1021/acs.jpcc.7b09820

Cartwright JHE, Checa AG, Gale JD, Gebauer D, Sainz-Díaz CI (2012) Calcium carbonate polyamorphism and its role in biomineralization: How many amorphous calcium carbonates are there? Angewandte Chemie International Edition 51: 11960-11970, doi: 10.1002/anie.201203125

Demichelis R, Raiteri P, Gale JD, Quigley D, Gebauer D (2011) Stable prenucleation mineral clusters are liquid like ionic polymers. Nature Communications 2: 590, doi: 10.1038/ncomms1604

De Yoreo JJ and 10 coauthors (2015) Crystallization by particle attachment in synthetic, biogenic, and geologic environments. Science 349: aaa6760, doi: 10.1126/ science.aaa6760

Dey A and 6 coauthors (2010) The role of pre-nucleation clusters in surface induced calcium phosphate crystallization. Nature Materials 9: 1010-1014, doi: 10.1038/ nmat2900

Gebauer D, Kellermeier M, Gale JD, Bergström L, Cölfen H (2014) Pre-nucleation clusters as solute precursors in crystallisation. Chemical Society Reviews 43: 2348-2371, doi: 10.1039/ C3CS60451A

Gebauer D, Raiteri P, Gale JD, Cölfen H (2018) On classical and nonclassical views on nucleation. American Journal of Science 318: 969-988, doi: 10.2475/09.2018.05

Gebauer D, Gale JD, Cölfen H (2022) Crystal nucleation and growth of inorganic ionic materials from aqueous solution: selected recent developments, and implications. Small 18: 2107735, doi: 10.1002/ smll.202107735

Gower LB (2008) Biomimetic model systems for investigating the amorphous precursor pathway and its role in biomineralization. Chemical Reviews 108: 4551-4627, doi: 10.1021/cr800443h

Ihli J and 7 coauthors (2014) Dehydration and crystallization of amorphous calcium carbonate in solution and in air. Nature Communications 5: 3169, doi: 10.1038/ ncomms4169

Jehannin M, Rao A, Cölfen H (2019) New horizons of nonclassical crystallization. Journal of the American Chemical Society 141: 10120-10136, doi: 10.1021/ jacs.9b01883

Koskamp JA and 6 coauthors (2024) The impact of stoichiometry on the initial steps of crystal formation: stability and lifetime of charged triple‐ion complexes. Chemistry A European Journal 30: e202303860, doi: 10.1002/chem.202303860

Meldrum FC, Cölfen H (2008) Controlling mineral morphologies and structures in biological and synthetic systems. Chemical Reviews 108: 4332-4432, doi: 10.1021/ cr8002856

Navrotsky A (2004) Energetic clues to pathways to biomineralization: precursors, clusters, and nanoparticles. Proceedings of the National Academy of Sciences 101: 12096-12101, doi: 10.1073/ pnas.0404778101

Parkhurst DL, Appelo CAJ (2013) Description of input and examples for PHREEQC version 3: a computer program for speciation, batch reaction, one dimensional transport, and inverse geochemical calculations. U.S. Geological Survey, 497 pp

Raiteri P, Gale JD (2010) Water is the key to nonclassical nucleation of amorphous calcium carbonate. Journal of the American Chemical Society 132: 17623-17634, doi: 10.1021/ja108508k

Raiteri P, Schuitemaker A, Gale JD (2020) Ion pairing and multiple ion binding in calcium carbonate solutions based on a polarizable AMOEBA force field and ab initio molecular dynamics. Journal of Physical Chemistry B, doi: 10.1021/acs. jpcb.0c01582

Rickard D, Luther GW (2007) Chemistry of iron sulfides. Chemical Reviews 107: 514-562, doi: 10.1021/cr0503658

Rudolph WW, Irmer G, Hefter GT (2003) Raman spectroscopic investigation of speciation in MgSO4(aq). Physical Chemistry Chemical Physics 5: 5253, doi: 10.1039/b308951g

Ruiz-Agudo E, Putnis CV, Putnis A (2014) Coupled dissolution and precipitation at mineral–fluid interfaces. Chemical Geology 383: 132-146, doi: 10.1016/j. chemgeo.2014.06.007

Schröder D and 5 coauthors (2011) Direct observation of triple ions in aqueous solutions of nickel(II) sulfate: a molecular link between the gas phase and bulk behavior. Journal of the American Chemical Society 133: 2444-2451, doi: 10.1021/ja105408a

Schuitemaker A, Koziara KB, Raiteri P, Gale JD, Demichelis R (2024) New model for aspartic acid species in aqueous calcium carbonate growth environments challenges and perspectives. Physical Chemistry Chemical Physics 26: 4909-4921, doi: 10.1039/D3CP04674E

Seepma SYMH and 5 coauthors (2021) Controlling CaCO3 particle size with {Ca2+}:{CO3 2–} ratios in aqueous environments. Crystal Growth & Design 21: 1576-1590, doi: 10.1021/acs.cgd.0c01403

Seepma SYMH, Kuipers BWM, Wolthers M (2023) Impact of solution {Ba2+}:{SO4 2–} on charge evolution of forming and growing barite (BaSO4) crystals: a ζ― potential measurement investigation. ACS Omega 8: 43521-43537, doi: 10.1021/ acsomega.3c03727

Smeets PJM and 5 coauthors (2017) A classical view on nonclassical nucleation. Proceedings of the National Academy of Sciences 114: E7882-E7890, doi: 10.1073/ pnas.1700342114

Stawski TM and 6 coauthors (2019) The structure of CaSO4 nanorods: the precursor of gypsum. The Journal of Physical Chemistry C 123: 23151-23158. doi: 10.1021/acs.jpcc.9b04268

Van Driessche AES, Stawski TM, Kellermeier M (2019) Calcium sulfate precipitation pathways in natural and engineered environments. Chemical Geology 530: 119274, doi: 10.1016/j. chemgeo.2019.119274

Wallace AF and 8 coauthors (2013) Microscopic evidence for liquid–liquid separation in supersaturated CaCO3 solutions. Science 341: 885-889, doi: 10.1126/science.1230915

Wolthers M, Van Der Gaast SJ, Rickard D (2003) The structure of disordered mackinawite. American Mineralogist 88: 2007-2015, doi: 10.2138/am 2003-11-1245