Uncertainty and Value: Optimising Geometallurgical Performance Along the Mining Value Chain

1811-5209/23/0019-0377$2.50  DOI: 10.2138/gselements.19.6.377

Keywords: Geometallurgy; raw materials value chain; stochastic modelling; optimisation; uncertainty

INTRODUCTION

The goal of all geometallurgical programs is to achieve optimal economic, environmental, and social outcomes along the whole value chain from ore to final product(s) and waste (cf. Frenzel et al. 2023 this issue). To reach this goal, geometallurgical modelling and optimisation must integrate all relevant data on the geology and primary characteristics of an ore deposit (cf. Butcher et al. 2023 this issue) with models that describe ore behaviour in downstream mineral processing and extractive metallurgy operations (cf. Pereira et al. 2023 this issue; Chetty et al. 2023 this issue). This article focuses on the integration of knowledge to develop and optimise a mine design, i.e., the specific layout of the mine and process flowsheet, and a mine plan or mine schedule, i.e., the order in which different parts of the deposit are mined.

The foundation for all mine planning and optimisation efforts generally is a well-defined mineral resource or reserve. We therefore start by describing how this is delineated, and then explain the standard routines currently used for mine design and planning. Because sampling, and therefore knowledge, of the heterogeneous geological bodies forming a mineral deposit is always incomplete, uncertainties arise on the distribution of specific rock properties within the deposit, as well as their effects on downstream operations. If ignored, these uncertainties can lead to detrimental operational decisions, and potentially negative economic, environmental, and/ or social outcomes. Therefore, the second part of this article describes how these uncertainties can be inferred and incorporated into the decision-making process to jointly (i.e., simultaneously and considering their interactions) optimise all stages of the value chain. The article closes with an account of the main aspects in uncertainty management and joint optimisation with geometallurgical data and models, which remain unresolved in both current industrial practice and academic research.

MINERAL RESOURCES AND RESERVES

Mineral resources are proven volumes of a geological material with a quality and quantity that provide reasonable prospects for eventual economic extraction. Resources are delineated with relevant geological information (typically assayed samples from drill cores and geological mapping) according to technical guidelines set out by regulatory committees (e.g., Australasian Joint Ore Reserves Committee 2012; Pan-European Reserves & Resources Reporting Committee 2021). They are generally classified into three standardised categories—measured, indicated, and inferred—in order of increasing level of uncertainty. Mineral resources chiefly reflect the geology of a deposit and the degree to which it has been explored.

In contrast to mineral resources, reserves are defined as the economically extractable part of the measured and/or indicated resources. Probable and proven reserve categories are distinguished—with increasing certainty that extraction becomes feasible. The estimation of reserves considers not only the presence of a certain amount of ore in the ground but also demonstrates its economic potential through a pre-feasibility or a feasibility study, where all technical constraints imposed by a specific mine design are considered (Canadian Institute for Mining, Metallurgy and Petroleum 2014). Technical constraints typically include, for instance, achievable metal recoveries or slope stability in an open pit. The economic feasibility assessment also accounts for external risks linked to geopolitical and market conditions (expected prices, supply and demand), and policy aspects (social and environmental), among others. Because mineral reserves depend on a specific mine design, their delineation is already the outcome of an optimisation process.

MINE PLANNING AND OPTIMISATION

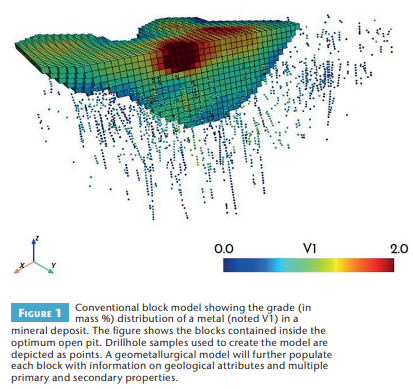Several models are required to develop a mine design and infer mineral resources and reserves. These are typically constructed with limited sample data, usually obtained from exploration drill holes (Fig. 1). A geological model of an ore deposit is generally built from drill core logs of geological attributes. It represents an interpretation of the location and extent of rock volumes with consistent properties within the deposit, also termed domains, such as a homogeneous lithology with a certain assemblage and abundance of minerals. Measured data on primary (cf. Butcher et al. 2023 this issue) and secondary (cf. Pereira et al. 2023 this issue) ore characteristics are then used to infer the properties of the rock within these domains and build a block model (Fig. 1).

A block model consists of volumes, usually regular in size, populated with rock property values inferred from the sample data. Each block should ideally contain values for all logged geological attributes as well as primary ore characteristics (e.g., concentrations of different elements, mineralogy, texture). However, in current practice mostly only the grades of the main commodities are used, while strategies to populate the block models with many of the properties mentioned above are still the subject of active research (van den Boogaart and Tolosana-Delgado 2018). Metallurgical test data on laboratory and pilot scales, together with appropriate process models (cf. Pereira et al. 2023 this issue), are often used to link the inferred primary characteristics to secondary characteristics for each block (e.g., hardness, metal recovery, acid consumption) for any given mine design and process flowsheet, such that mineto-plant optimisation becomes possible (Ortiz et al. 2015). This optimisation generally proceeds from the larger to the smaller scale, first choosing a mine design and long-term mine plan, then optimising the performance of that design over the shorter term.

Mine Design and Mine Plan

To choose the best mine design and optimise the mine plan, different designs and process flowsheets must be compared, and the mine plan optimised for each. To do so, each block in the block model must be assigned an economic value, which depends on its properties. This is typically done via a formula of the form:

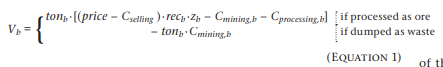
where Vb represents the value of block b, tonb represents its tonnage, price is the commodity price, Cselling considers any selling, transportation, or refining costs per tonne, recb and zb are the recovery and commodity grade of the block, respectively, and Cmining,b and Cprocessing,b are the respective mining and processing costs per tonne for the specific block and design. Note that this calculation generally will also need to account for the effects of blending different ore blocks before processing, a procedure currently used to reduce the variability of feed properties for downstream operations. Indeed, the industry standard is to filter out ore variability with blending, disregarding the additional profit that predictive adaption can provide (Tolosana-Delgado et al. 2015).

The value of the blocks is used to determine the economic outline of the deposit, that is, the envelope that can be economically mined out by surface or underground mining methods, and that maximises the total obtained economic value at a given moment. This is usually done by considering the undiscounted value of the blocks extracted, i.e., not accounting for the time value of money (cf. Frenzel et al. 2023 this issue). This approach allows for a simple determination of the mining limits to maximise the value obtained from the extraction of the ore. Furthermore, in that optimisation, accessibility needs to be considered as a constraint when deciding which blocks can be extracted. In an open pit, this requires removing the overlying blocks and accessing through a ramp. In underground mining, it requires developing access to the corresponding production point.

Once the limits of the ore bodies have been determined, the sequence of extraction of the blocks, i.e., the mine plan, can be optimised by considering the life-of-mine and the time value of money, and determining in which period each block should be removed. The sequence is optimised to maximise the discounted profit obtained from mining out the reserves, resulting in an assessment of the potential value of the entire operation, expressed as net present value (NPV, cf. Frenzel et al. 2023 this issue), for all optimal combinations of different mine designs and mine plans. Based on the comparison of these NPVs, the optimal design and schedule can be chosen. Environmental aspects, such as CO2 emissions, can also be incorporated into the optimisation routine in addition to economic value (cf. Pell et al. 2019).

System Optimisation

Once a mine has been built and the operation is running, the properties and process responses of the different material streams generally become better known. The stages of the process flowsheet can then be optimised on a smaller timescale (weeks, days, shifts) to enhance their performance and reduce potential deviations from the long-term mine plan. This partial optimisation process aims to fine-tune specific process parameters, including ore blending, without necessarily changing the mine plan. The process is best illustrated with two examples.

Example 1: Mine to mill optimisation focuses on the combined cost of blasting and comminution to achieve a specific particle size. Using more explosives will generate run-of-mine ore with a smaller particle size, which will reduce the amount of energy consumed during crushing and grinding. Alternatively, one can reduce the explosive consumption and generate coarser run-of-mine ore that will require more energy for comminution. However, both processes produce different particle size distributions. In particular, the excessive use of explosives in blasting may generate unmanageable amounts of unrecoverable fines. Therefore, a joint optimisation routine must be used to identify the ideal ratio of the relative energy expenditures in blasting and comminution to maximise mineral liberation and minimise total cost, emissions, and energy consumption.

Example 2: Product specification optimisation is illustrated in Figure 2. As explained in Pereira et al. (2023 this issue), flotation performance depends on the composition of an ore, the liberation degree of the particles, and the specific operational settings of the processing plant (Fig. 2A). These settings are controlled by an operator based on the expected characteristics of the feed to the flotation process. However, ore types usually have highly variable properties. Some types may require a higher amount of energy to be milled to a specific particle size. Two options can then be considered (Fig. 2C): (1) decrease mill throughput to ensure the materials have a larger residence time in the mill and thereby achieve the expected degree of liberation; or (2) retain current mill throughput, thereby generating a coarser product in which the ore minerals are less liberated.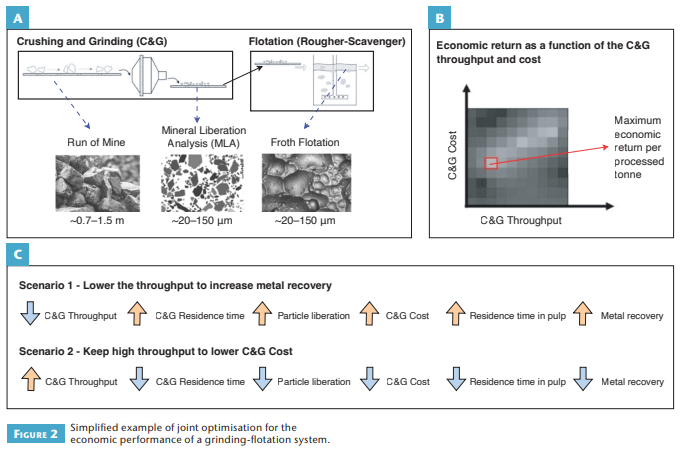

Each approach will have consequences for the resulting downstream processes. Reduced throughput will often enhance recovery due to better liberation of the ore minerals and increased residence time in the flotation cells. However, economic performance may worsen because of the smaller amount of material treated per time unit, which generates lower revenues. In the second case, particles are coarser, which negatively affects flotation because ore minerals may not be fully liberated. However, the increased throughput may counter this effect, as well as some of the associated revenue loss, through the larger volume of ore being processed per time unit. The process can be optimised to find the throughput level that maximises the expected economic performance of grinding and flotation simultaneously (Fig. 2B). Microstructure-aware processing models (Pereira et al. 2023 this issue) could help here. These are only two simple examples of specific subprocesses that illustrate some of the interactions between different parts of the process chain. In the end, the optimal operating conditions for the entire chain should be found by jointly optimising the parameters of all relevant subprocesses. This is typically done using process models and simulations.

UNCERTAINTIES AND THEIR CONSEQUENCES

In the past, the optimisation routines described above were usually conducted using best-fit values for all inferred quantities. That is, the separate distributions of a handful of primary ore characteristics within the deposit were modelled with simple interpolation routines, such as inverse distance-weighted interpolation or kriging (Matheron 1963), giving a single best estimate of the primary ore properties for each block in the block model. Secondary characteristics of the blocks were then inferred from process models, again assigning only best estimates. The subsequent optimisation process naturally yielded a single optimal mine design and plan. This approach is still widely used in the mining industry.

However, the inputs to the optimisation of a mining project generally are highly uncertain and multivariate. Only a small proportion of a given mineral deposit can be sampled and analysed in a feasible manner, and the typically heterogeneous nature and spatial variability of the deposit mean that the ore between sample locations will not have identical characteristics to the available samples (cf. Box 1). Traditional interpolation methods smooth out this heterogeneity, producing modelled property distributions that do not correspond with real geological features. Furthermore, the distribution of metal grades generally is much better known than the distribution of many key mineralogical and textural properties, as well as secondary ore characteristics, as acquiring detailed data on the former properties is much cheaper (cf. Butcher et al. 2023 this issue).

Similarly, process models generally have large residual uncertainties (Rossi and Deutsch 2014). The reasons for this lie both in the usually limited availability of metallurgical test data and the inability of typical predictor variables used in current process models to account for the variations in relevant ore characteristics. The chemical composition of an ore may be a reasonable proxy for its mineralogical composition, and thus some secondary ore properties such as hardness, but is a poor proxy for ore texture and the resultant liberation behaviour of the ores (cf. Pereira et al. 2023 this issue).

It follows from these considerations that the uncertainties arising for the primary properties of each block and its process behaviour can be substantial. The important question is what effects these uncertainties have on the outcomes of optimisation routines. Will the optimal design and schedule derived from the best-fit (or average) properties of the deposit still provide the best option?

Much research has been done over the last decade to investigate this problem, showing that variability and uncertainty greatly affect the performance of a mining operation, and that ignoring them will systematically decrease both product quality and quantity with respect to the expectations based on a traditional mine design and mine plan (Dimitrakopoulos 2011; Leite and Dimitrakopoulos 2014). The chief reason for this is that the process behaviour of each block is a non-linear function of its primary properties. As a simplified example, consider the block value (Eq. 1) as the target response: here, the problem arises mainly because recovery and processing costs non-linearly depend on grade, but also because blocks are dumped if their value is below a certain threshold, hence the block value no longer depends on grade. Most importantly, all these costs depend on a wide range of geometallurgical properties, not just grade. This is why geometallurgical optimisation must account for uncertainties to ensure that the best decisions are made. The following section describes how this can be achieved.

UNCERTAINTY MODELLING AND STOCHASTIC OPTIMISATION

To adequately account for uncertainties in the development and optimisation of a mine design and mine plan, two things are required: 1) adequate models of the relevant uncertainties; and 2) a stochastic optimisation routine, which can deal with the uncertain inputs generated by uncertainty modelling

Uncertainty Modelling

As noted above, uncertainties mainly arise in two different parts of a mining operation. First, there is geospatial uncertainty due to the intrinsic spatial variation of ore properties throughout the ore deposit, along with limited informationfrom samples to allow its characterisation. This geospatial uncertainty is subsequently translated into temporal uncertainty regarding the properties of the feed materials sent for downstream processing once the ore has been extracted. Second, due to the limitations of current process models, the responses of the ores in the mineral processing and extractive metallurgical stages are uncertain, even if their primary characteristics are well known. This effect is exacerbated by the first source of uncertainty, i.e., the incomplete knowledge of the primary characteristics of the feed material. A third source of uncertainty is the limited knowledge of external factors relevant to the decisions made in a mining project, including future commodity prices, labour costs, access to water and energy, etc.

Box 1 GEOSTATISTICS FOR MODELLING GEOSPATIAL UNCERTAINTY

Geostatistics provides a set of tools to find local estimates (predictions) and to characterise uncertainty for spatially distributed continuous and categorical variables. Geostatistical techniques are based on a probabilistic approach (Matheron 1963), where properties are modelled as random variables, that is, they can take values according to a certain probability distribution. If an attribute is known at a given location through sampling, it has only analytical uncertainties (Butcher et al. 2023 this issue). On the other hand, attributes at unsampled locations are estimated through a weighted average of the neighbouring known sample values, assumed to belong to the same statistical population and behave as a stationary variable in space:

where Z*(u0) is the estimated value at location u0, λ0, … , λn are weights that need to be determined, and Z*(u1), … , Z*(un) are the values of the n neighboring samples around u0. Kriging is the method used to determine the weights λ0, … , λn, imposing global unbiasedness, and optimality, with the latter being defined as the minimisation of the error variance between the estimate and the true (but unknown) value:

Solving for the weights requires characterising the spatial continuity of the random function (the collection of random variables in the spatial domain). This is achieved through the use of a variogram model, which measures how much the attribute can change when comparing locations separated by a given lag vector h. Kriging provides only best estimates of the values at unknown locations (best-fit values). Under certain assumptions, the full probability distributions of the random variables at unsampled locations can be characterised, providing a quantification of the uncertainty around the best-fit value. This notion is extended to account for joint spatial uncertainty, through geostatistical simulation conditional to the known samples at their locations. Each simulation respects the sample data, honours the global distribution of the attribute, and reproduces the spatial continuity, as characterised by the variogram. This can be used to quantify uncertainty over volumes such as mining blocks.

In geometallurgical modelling, simulations must consider multiple attributes co-varying in space (termed cosimulation) to capture their statistical and spatial relationships in a geometallurgical assessment (Wackernagel 2003). Most cosimulation techniques decompose the multivariate relationships into a set of factors that can be modelled independently, thus simplifying the simulation process (Desbarats and Dimitrakopoulos 2000; Leuangthong and Deutsch 2003; Barnett et al. 2014). When some variables describe the ore composition (e.g., mineralogical or chemical), a previous log-ratio transformation is often required, and compositional data analysis tools can be used (Tolosana-Delgado et al. 2019). These techniques generate multiple scenarios for the spatial joint distribution of variables, respecting their sample values at sample locations, and reproducing their multivariate spatial distributions, i.e., the spatial continuity of the variables and spatial cross-correlation between them (Boisvert et al. 2013). These techniques can also be extended to categorical variables (e.g., lithologies, alteration styles, geological domains), where specific geostatistical simulation techniques generate a prediction of the probability of a location belonging to each of the several categories considered.

Geospatial uncertainties are typically modelled using geostatistical tools (see Box 1). These tools include classical interpolation routines such as kriging, as well as the possibility to generate simulations, or realisations, of more realistic potential property distributions within the deposit (cf. Fig. 3 of Frenzel et al. 2023 this issue). Each realisation is equally likely to be true and assigns a single value of each modelled property to each block in the deposit model. An ensemble of such realisations can be used to represent the overall geospatial uncertainties.In the next step, process responses or secondary characteristics must be assigned to each block in each realisation. For this purpose, process models and their residual uncertainties can be used (cf. Pereira et al. 2023 this issue). To build these models, the behaviour of the ore streams is initially characterised through small-scale tests, which are then complemented by on-site measurements to understand how they scale to actual production volumes (Chetty et al. 2023 this issue). One issue with most process models in current use is that they are often aimed at predicting the expected value of a response property based on simple bulk chemical measurements, and do not account for the actually relevant geometallurgical properties.

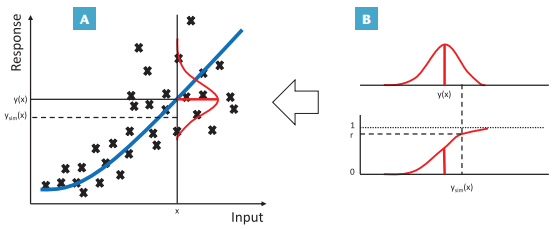
To transfer the residual uncertainty of the responses from classical process models to the block model, a Monte-Carlo approach may be used. This is illustrated in Figure 3, which presents a simplified model of a hypothetical non-linear response given a primary variable. Models typically provide a best-fit estimate of the response y(x) for a given input x. However, actual responses will generally fluctuate around the estimate of y(x) according to a certain distribution. This distribution of the residual values can be modelled, allowing for the random sampling of a value from that distribution, ysim(x), for any given value of x. This process can be repeated for each block in each of the realisations of the deposit generated from geostatistical simulation to yield overall realisations of the block model (cf. Fig. 3 in Frenzel et al. 2023 this issue), which, in turn, can be used in mine planning and optimisation.

Finally, different scenarios are constructed for the development of external factors such as market prices and regulatory environments. These can be used for stochastic optimisation in combination with the different realisations of the block model.

Stochastic Optimisation

Here, the goal of stochastic optimisation is to find the mine design and mine plan that maximise the deposit value and minimise environmental and social impacts (Leite and Dimitrakopoulos 2014). This can be achieved by first defining a set of concrete mine designs and mine plans. Each of these design/plan combinations is then applied to all realisations of the block model, under all pre-defined scenarios for the external factors (Fig. 4), to yield a probability distribution of the target performance indicator (e.g., NPV, emissions). These distributions are then compared, and the best design/ plan combination is selected according to predefined risk criteria. Specifically, the mean or median of the distribution indicates the expected system performance for a specific combination, while the width and shape reflect the associated risks. Generally, the optimal design/plan combination will maximise the expected performance indicator subject to a tolerable associated risk. For a predefined risk level, stochastic optimisation allows finding the design/plan with the best performance. Alternatively, for a fixed performance, the model with the lowest risk can be identified.

UPDATING OF MODELS AND MINE PLANS

The previous discussion implicitly assumed that the amount of data available for the optimisation of a mining operation is fixed. However, in operating mines and associated beneficiation plants, a wealth of new data on both primary and secondary properties is continuously acquired. For instance, face mapping and production drilling generate detailed data on the geology and chemical composition of blocks just before they are blasted and processed. Online sensors in the mineral processing plant record information on chemistry, particle size distributions, reagent consumption, etc. of the various process streams. Overall metal recoveries, energy consumption, and other performance parameters of the processing plant are also typically monitored in real time.

This wealth of data, in principle, allows for the monitoring of the performance of specific volumes of ore as they pass through the process chain, and for comparison with model predictions. The data should, therefore, be used to update the various ore body and process models in real time. This is vital to reduce the uncertainties about the attributes of each mining block, the performance of the processes downstream, and the best short-term decisions (Wambeke et al. 2018; Benndorf 2020). Such updating will require fast, smart sensors and smart measurements, high-speed communication to transfer information, indirect (soft) sensors, computational infrastructure with dedicated software, and so-far non-existing methods to update models and decisions. Once properly calibrated and trained, an automated agent could assume control over decision-making processes to optimise both individual processes and overall system performance.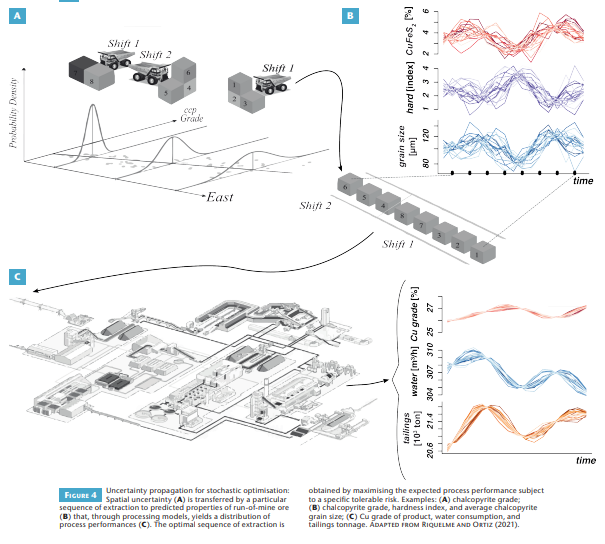

Unfortunately, such technology is currently only in place in some beneficiation plants, and even there the data are not used to update the block model or to re-optimise the full system.

SUMMARY AND OUTLOOK

Geometallurgical modelling should help to integrate knowledge and improve decision-making at all stages of the raw materials value chain. This is not yet the case: much of the mining industry continues to operate by defining performance metrics at each processing stage independently, where each stage is optimised disregarding the impact on other stages. This has slowly started to change, given the obvious benefits of jointly optimising the whole value chain. However, the necessary transition is in its infancy, and there is still a lack of understanding about the effects of variability in process performance, and the impact of uncertainty in decision making.

This article provided a brief discussion of how uncertainty can be incorporated into the various models used for mine design and mine planning, and how the joint optimisation of different processes (or the entire value chain) can be achieved in the shadow of uncertainty. However, much work is still needed to fully implement such routines in automatic control systems. Implementation will require not only that boundaries between the traditional departments within mining companies are overcome, but also that interactions occur between different companies. The last aspect is critical to achieve full integration along the value chain, including extractive metallurgy operations (Chetty et al. 2023 this issue), as these are often located at different sites and are owned by different companies. Another area for future research is the improvement of uncertainty models, and development of methods and routines that can further reduce uncertainties. At present, four major factors hinder uncertainty reduction and uncertainty modelling:

• Limited sampling and limited sample quality at different stages of the various process streams. Particularly high-frequency online measurements of ore properties (directly relevant or proxies) are needed for real-time process control and uncertainty reduction.
• Limited analytical capabilities to acquire not only large amounts of data, but large amounts of the right data, such as mineralogical and textural information (cf. Butcher et al. 2023 this issue), which is much more relevant to the modelling of processing operations than bulk chemical data (cf. Pereira et al. 2023 this issue). This is currently limited by the availability and cost of suitable technology.
• Limited process understanding. As discussed in detail in Pereira et al. (2023 this issue), there are currently some major gaps in process models, particularly those used for comminution processes, which limit their ability to incorporate detailed data on ore mineralogy and texture. This imposes limitations on both the modelling of the processes (uncertainty reduction) and the understanding and quantification of the uncertainties that arise during this modelling, all effects that are compounded by the limited availability of relevant analytical data (see previous point).
• Limited geospatial modelling techniques exist that can deal with geometallurgical variables, such as texture, modal mineralogy, or deportment. New multivariate interpolation and simulation methods will be needed to ensure full incorporation of these properties into the geometallurgical block models.

If these limitations are overcome, more robust geometallurgical models may be constructed to make mining operations more sustainable, maximising the recovery of relevant commodities, while minimising the potential negative impacts of their extraction and ensuring the responsible use of land, water, and energy. This can be extended to the re-processing and valorisation of mine wastes (cf. Parbhakar-Fox and Baumgartner 2023 this issue).

ACKNOWLEDGMENTS

We would like to thank the guest editors of this Elements issue for their invitation to contribute this article. Furthermore, we are indebted to reviewers Jeff Boisvert and Hassan Talebi for their constructive comments, which helped us to significantly improve the original manuscript. All authors would like to acknowledge the funding provided by Queen’s University, SRK Consulting (Canada) Inc., Nazarbayev University, and HZDR. In particular, Dr. Madani acknowledges Nazarbayev University via Faculty Development Competitive Research Grants for 2021–2023, grant number 021220FD4951 for partially funding this work.

REFERENCES

Australasian Joint Ore Reserves Committee (2012) The Australasian Code for Reporting of Exploration Results, Mineral Resources and Ore Reserves. Australian Institute of Geoscientists and Mineral Council of Australia, 44 pp

Barnett RM, Manchuk JG, Deutsch CV (2014) Projection pursuit multivariate transform. Mathematical Geosciences 46: 337-359, doi: 10.1007/s11004-013-9497-7

Benndorf J (2020) Closed Loop Management in Mineral Resource Extraction: Turning Online Geo-Data into Mining Intelligence. Springer Nature, 104 pp

Boisvert J, Rossi ME, Ehrig K, Deutsch CV (2013) Geometallurgical modeling at Olympic Dam Mine, South Australia. Mathematical Geosciences 45: 901-925, doi: 10.1007/s11004-013-9462-5

Butcher AR, Dehaine Q, Menzies AH, Michaux SP (2023) Characterisation of ore properties for geometallurgy. Elements 19: 352-358

Canadian Institute for Mining, Metallurgy and Petroleum (2014) CIM Definition Standards for Mineral Resources and Mineral Reserves. Canadian Institute of Mining, Metallurgy and Petroleum, 9 pp

Chetty D, Nwaila GT, Xakalashe B (2023) Fire and water: geometallurgy and extractive metallurgy. Elements 19: 365-370

Desbarats A, Dimitrakopoulos R (2000) Geostatistical simulation of regional-ized pore-size distributions using min/max autocorrelation factors. Mathematical Geology 32: 919-942, doi: 10.1023/A:1007570402430

Dimitrakopoulos R (2011) Stochastic optimization for strategic mine planning: a decade of developments. Journal of Mining Science 47: 138-150, doi: 10.1134/ S1062739147020018

Frenzel M, Baumgartner R, Tolosana-Delgado R, Gutzmer J (2023) Geometallurgy: present and future. Elements 19:345-351

Leite A, Dimitrakopoulos R (2014) Stochastic optimization of mine production sched-uling with uncertain ore/metal/waste supply. International Journal of Mining Science and Technology 24: 755-762, doi: 10.1016/j.ijmst.2014.10.004

Leuangthong O, Deutsch CV (2003) Stepwise conditional transformation for simulation of multiple variables. Mathematical Geology 35: 155-173, doi: 10.1023/A:1023235505120

Matheron G (1963) Principles of geostatis – tics. Economic Geology 58: 1246-1266, doi: 10.2113/gsecongeo.58.8.1246

Ortiz JM and 6 coauthors (2015) Workflows in geometallurgical prediction: challenges and outlook. In: Schaeben H, Tolosana Delgado R, van den Boogaart KG, van den Boogaart R (eds) Proceedings of the 17th Annual Conference of the International Association for Mathematical Geosciences IAMG, pp 228-233

Pan-European Reserves & Resources Reporting Committee (2021) Pan- European Standard for the Public Reporting of Exploration Results, Mineral Resources and Mineral Reserves. Committee for Mineral Reserves International Reporting Standards, 98 pp

Parbhakar-Fox A, Baumgartner R (2023) Action versus reaction: how geometal-lurgy can improve mine waste manage-ment across the life-of-mine. Elements 19: 371-376

Pell R and 7 coauthors (2019) Environmental optimisation of mine scheduling through life cycle assessment integra-tion. Resources, Conservation & Recycling 142: 267-276, doi: 10.1016/j. resconrec.2018.11.022

Pereira L, Schach E, Tolosana-Delgado R, Frenzel M (2023) All about particles: modelling ore behaviour in mineral processing. Elements 19: 359-364

Riquelme AI, Ortiz JM (2021) Uncertainty assessment over any volume without simulation: revisiting multi-Gaussian kriging. Mathematical Geosciences 53: 1375-1405, doi: 10.1007/ s11004-020-09907-9

Rossi ME, Deutsch CV (2014) Mineral Resource Estimation. Springer, 332 pp

Tolosana-Delgado R, Mueller U, van den Boogaart KG, Ward C, Gutzmer J (2015) Improving processing by adaption to conditional geostatistical simulation of block compositions. Journal of the South African Institute of Mining and Metallurgy 115: 13-26

Tolosana-Delgado R, Mueller U, van den Boogaart KG (2019) Geostatistics for compositional data: an overview. Mathematical Geosciences 51: 485-526, doi: 10.1007/s11004-018-9769-3

van den Boogaart KG, Tolosana-Delgado, R (2018) Predictive geometallurgy: an interdisciplinary key challenge for mathematical geosciences. In: Daya Sagar BS, Cheng Q, Agterberg F (eds) Handbook of Mathematical Geosciences. Springer, Cham, pp 673-686

Wackernagel H (2003) Multivariate Geostatistics: An Introduction with Applications. Springer, 388 pp

Wambeke T, Elder D, Miller A, Benndorf J, Peattie R (2018) Real- time reconciliation of a geometallurgical model based on ball mill performance measurements–a pilot study at the Tropicana gold mine. Mining Technology 127: 115-130, doi: 10.1080/25726668.2018.1436957